Sparse Matrix Containers

Just like sparse matrices store individual scalars, bsparse’s sparse matrix containers generalize this concept to storing arbitrary-type 2D sub-blocks.

This type of coarse-grained sparsity structure is often found in deep learning applications, in regression calculations, in finite-element discretizations, and in other discretizations of operators onto basis functions with small support.

It can be more natural to work with objects that can be accessed and modified block-by-block and one can also gain a computational advantage employing sparse matrix containers for certain algorithms like selected matrix inversion or selected matrix multiplication.

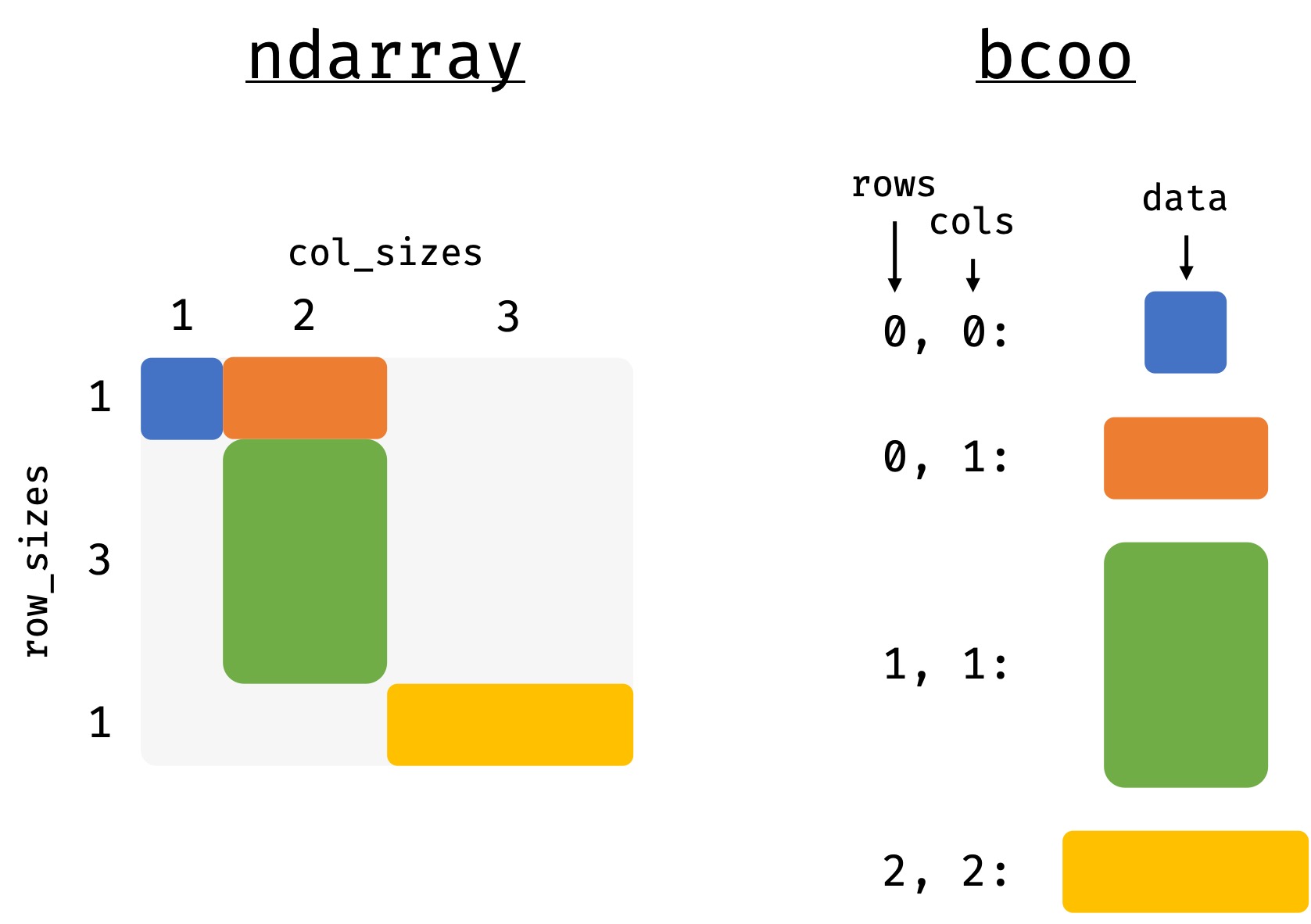
The sub-blocks in bsparse matrices have to be aligned, i. e. they must not be ragged. This way we can define a set of row-sizes (.row_sizes) and column-sizes (.col_sizes). The sub-blocks are aligned on the grid that these values span. To create a bsparse matrix from a dense array, we need to specify the row- and column-sizes.

>>> import bsparse as bsp
>>> import numpy as np
>>> arr = np.zeros((5, 6))
>>> arr[0, 0] = 1
>>> arr[0, 1:3] = 2
>>> arr[1:4, 1:3] = 3
>>> arr[-1, 3:] = 4
>>> arr
array([[1., 2., 2., 0., 0., 0.],
       [0., 3., 3., 0., 0., 0.],
       [0., 3., 3., 0., 0., 0.],
       [0., 3., 3., 0., 0., 0.],
       [0., 0., 0., 4., 4., 4.]])
>>> row_sizes = [1, 3, 1]
>>> col_sizes = [1, 2, 3]
>>> bcoo = bsp.BCOO.from_array(arr, (row_sizes, col_sizes))
>>> bcoo
BCOO(bshape=(3, 3), bnnz=4 | shape=(5, 6), nnz=12)

Like scalar-element sparse matrices, the corresponding dense array can be represented in several equivalent ways. The only difference is that the .data is now a list of sub-blocks rather than a dense array of scalars.

>>> bcoo.data
[
    array([[1.]]),
    array([[2., 2.]]),
    array([[3., 3.],
           [3., 3.],
           [3., 3.]]),
    array([[4., 4., 4.]])
]

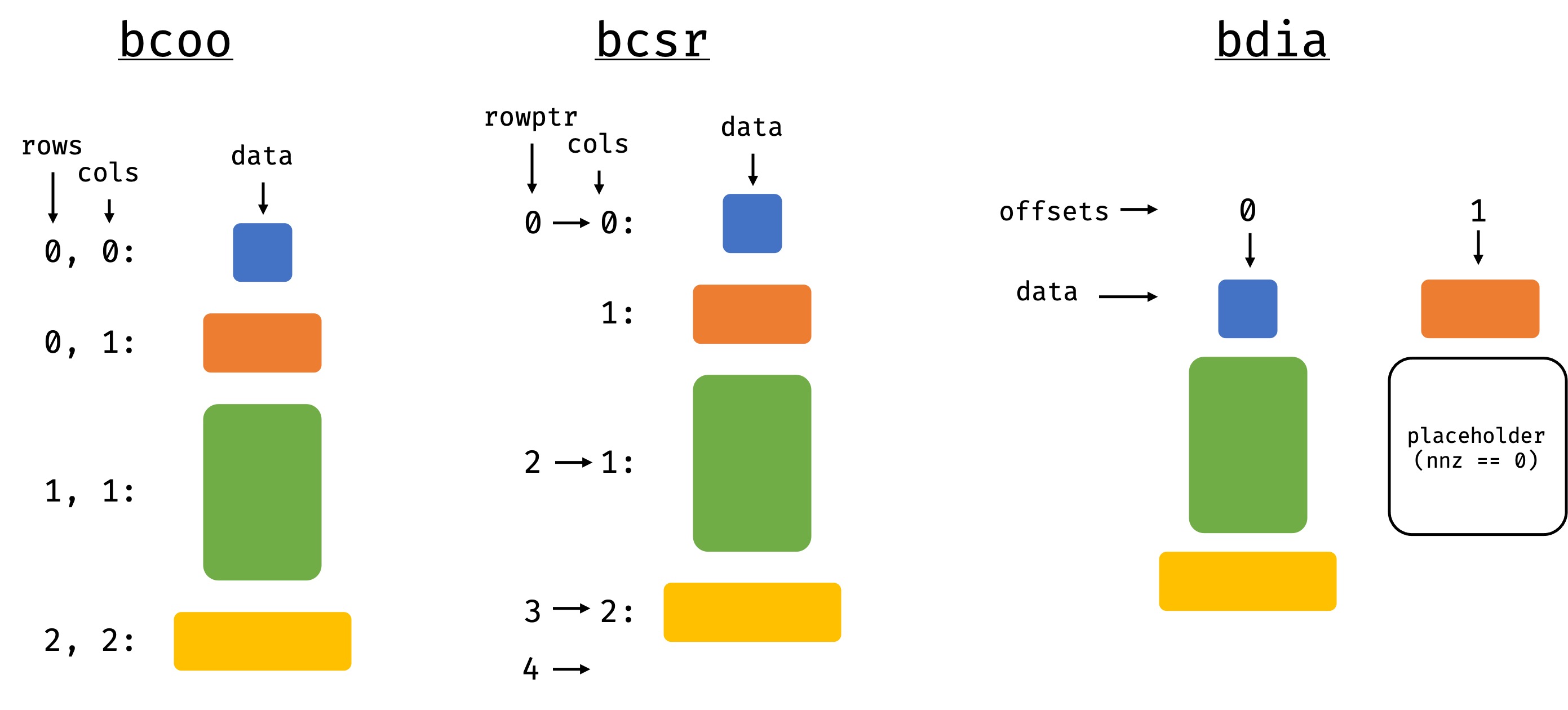
This can now be again converted to the different sparse representations.

>>> bcoo.tocsr()
BCSR(bshape=(3, 3), bnnz=4 | shape=(5, 6), nnz=12)
>>> bcoo.todia()
BDIA(bshape=(3, 3), bnnz=5 | shape=(5, 6), nnz=12)

All bsparse matrices have a datatype of the underlying scalars (.dtype), a 2D matrix shape (.shape), a number of explicitly stored values (.nnz), and a symmetry attribute (.symmetry).

>>> bcoo.dtype
dtype('float64')
>>> bcoo.shape
(5, 6)
>>> bcoo.nnz
12
>>> bcoo.symmetry  # None

In addition they have attributes describing the block-structure. These are the shape in terms of blocks (.bshape), the number of explicitly stored blocks (.bnnz), and the row- and column-sizes mentioned before.

>>> bcoo.bshape
(3, 3)
>>> bcoo.bnnz
4
>>> bcoo.row_sizes
array([1, 3, 1])
>>> bcoo.col_sizes
array([1, 2, 3])

Again, all arithmetic operations are supported.

>>> (bcoo * bcoo + 2*bcoo) @ bcoo.T
BCOO(bshape=(3, 3), bnnz=5 | shape=(5, 5), nnz=17)

In addition, the blocks stored in a bsparse matrix can be modified using the .bapply() function. This maps a callable argument onto all the stored blocks.

>>> >>> bcoo.bapply(lambda b: b**2)
BCOO(bshape=(3, 3), bnnz=4 | shape=(5, 6), nnz=12)